‘vector’ Dialect
MLIR supports multi-dimensional vector types and custom operations on those types. A generic, retargetable, higher-order vector type (n-D with n > 1) is a structured type, that carries semantic information useful for transformations. This document discusses retargetable abstractions that exist in MLIR today and operate on ssa-values of type vector along with pattern rewrites and lowerings that enable targeting specific instructions on concrete targets. These abstractions serve to separate concerns between operations on memref (a.k.a buffers) and operations on vector values. This is not a new proposal but rather a textual documentation of existing MLIR components along with a rationale.
Positioning in the Codegen Infrastructure
The following diagram, recently presented with the StructuredOps abstractions, captures the current codegen paths implemented in MLIR in the various existing lowering paths. 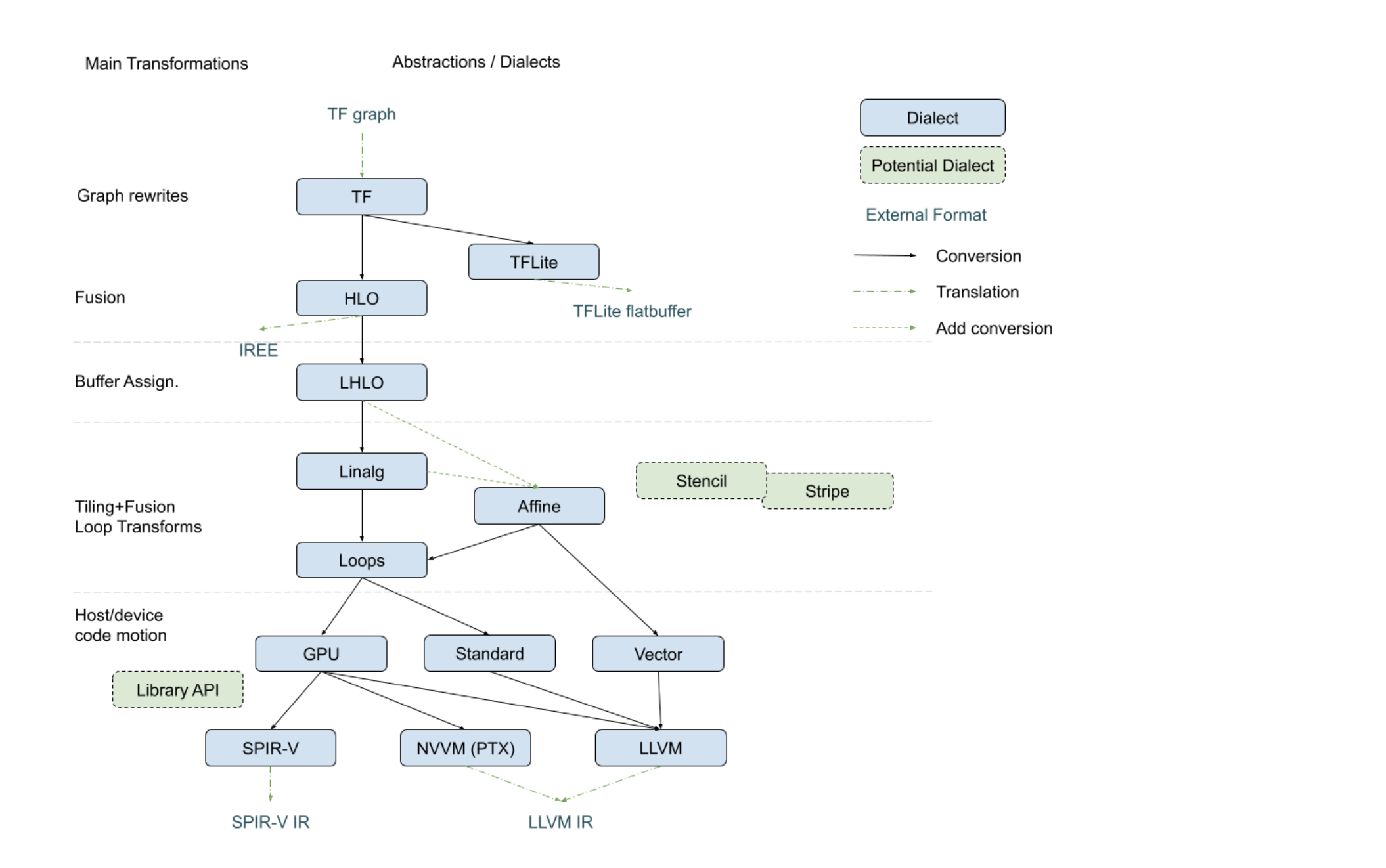
The following diagram seeks to isolate vector dialects from the complexity of the codegen paths and focus on the payload-carrying ops that operate on std and vector types. This diagram is not to be taken as set in stone and representative of what exists today but rather illustrates the layering of abstractions in MLIR.

This separates concerns related to (a) defining efficient operations on vector types from (b) program analyses + transformations on memref, loops and other types of structured ops (be they HLO, LHLO, Linalg or other ). Looking a bit forward in time, we can put a stake in the ground and venture that the higher level of vector-level primitives we build and target from codegen (or some user/language level), the simpler our task will be, the more complex patterns can be expressed and the better performance will be.
Components of a Generic Retargetable Vector-Level Dialect
The existing MLIR vector-level dialects are related to the following bottom-up abstractions:
- Representation in
LLVMIRvia data structures, instructions and intrinsics. This is referred to as theLLVMlevel. - Set of machine-specific operations and types that are built to translate almost 1-1 with the HW ISA. This is referred to as the Hardware Vector level; a.k.a
HWV. For instance, we have (a) theNVVMdialect (forCUDA) with tensor core ops, (b) accelerator-specific dialects (internal), a potential (future)CPUdialect to captureLLVMintrinsics more closely and other dialects for specific hardware. Ideally this should be auto-generated as much as possible from theLLVMlevel. - Set of virtual, machine-agnostic, operations that are informed by costs at the
HWV-level. This is referred to as the Virtual Vector level; a.k.aVV. This is the level that higher-level abstractions (codegen, automatic vectorization, potential vector language, ...) targets.
The existing generic, retargetable, vector-level dialect is related to the following top-down rewrites and conversions:
- MLIR Rewrite Patterns applied by the MLIR
PatternRewriteinfrastructure to progressively lower to implementations that match closer and closer to theHWV. Some patterns are “in-dialect”VV -> VVand some are conversionsVV -> HWV. Virtual Vector -> Hardware Vectorlowering is specified as a set of MLIR lowering patterns that are specified manually for now.Hardware Vector -> LLVMlowering is a mechanical process that is written manually at the moment and that should be automated, following theLLVM -> Hardware Vectorops generation as closely as possible.
Short Description of the Existing Infrastructure
LLVM level
On CPU, the n-D vector type currently lowers to !llvm<array<vector>>. More concretely, vector<4x8x128xf32> lowers to !llvm<[4 x [ 8 x [ 128 x float ]]]>. There are tradeoffs involved related to how one can access subvectors and how one uses llvm.extractelement, llvm.insertelement and llvm.shufflevector. A deeper dive section discusses the current lowering choices and tradeoffs.
Hardware Vector Ops
Hardware Vector Ops are implemented as one dialect per target. For internal hardware, we are auto-generating the specific HW dialects. For GPU, the NVVM dialect adds operations such as mma.sync, shfl and tests. For CPU things are somewhat in-flight because the abstraction is close to LLVMIR. The jury is still out on whether a generic CPU dialect is concretely needed, but it seems reasonable to have the same levels of abstraction for all targets and perform cost-based lowering decisions in MLIR even for LLVM. Specialized CPU dialects that would capture specific features not well captured by LLVM peephole optimizations of on different types that core MLIR supports (e.g. Scalable Vectors) are welcome future extensions.
Virtual Vector Ops
Some existing Standard and Vector Dialect on n-D vector types comprise:
%2 = arith.addf %0, %1 : vector<3x7x8xf32> // -> vector<3x7x8xf32> %2 = arith.mulf %0, %1 : vector<3x7x8xf32> // -> vector<3x7x8xf32> %2 = std.splat %1 : vector<3x7x8xf32> // -> vector<3x7x8xf32> %1 = vector.extract %0[1]: vector<3x7x8xf32> // -> vector<7x8xf32> %1 = vector.extract %0[1, 5]: vector<3x7x8xf32> // -> vector<8xf32> %2 = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32> // -> vector<4x8xf32> %3 = vector.outerproduct %0, %1, %2: vector<4xf32>, vector<8xf32> // fma when adding %2 %3 = vector.strided_slice %0 {offsets = [2, 2], sizes = [2, 2], strides = [1, 1]}: vector<4x8x16xf32> // Returns a slice of type vector<2x2x16xf32> %2 = vector.transfer_read %A[%0, %1] {permutation_map = (d0, d1) -> (d0)}: memref<7x?xf32>, vector<4xf32> vector.transfer_write %f1, %A[%i0, %i1, %i2, %i3] {permutation_map = (d0, d1, d2, d3) -> (d3, d1, d0)} : vector<5x4x3xf32>, memref<?x?x?x?xf32>
The list of Vector is currently undergoing evolutions and is best kept track of by following the evolution of the VectorOps.td ODS file (markdown documentation is automatically generated locally when building and populates the Vector doc). Recent extensions are driven by concrete use cases of interest. A notable such use case is the vector.contract op which applies principles of the StructuredOps abstraction to vector types.
Virtual Vector Rewrite Patterns
The following rewrite patterns exist at the VV->VV level:
- The now retired
MaterializeVectorpass used to legalize ops on a coarse-grained virtualvectorto a finer-grained virtualvectorby unrolling. This has been rewritten as a retargetable unroll-and-jam pattern onvectorops andvectortypes. - The lowering of
vector_transferops legalizesvectorload/store ops to permuted loops over scalar load/stores. This should evolve to loops overvectorload/stores +maskoperations as they become availablevectorops at theVVlevel.
The general direction is to add more Virtual Vector level ops and implement more useful VV -> VV rewrites as composable patterns that the PatternRewrite infrastructure can apply iteratively.
Virtual Vector to Hardware Vector Lowering
For now, VV -> HWV are specified in C++ (see for instance the SplatOpLowering for n-D vectors or the VectorOuterProductOp lowering).
Simple conversion tests are available for the LLVM target starting from the Virtual Vector Level.
Rationale
Hardware as vector Machines of Minimum Granularity
Higher-dimensional vectors are ubiquitous in modern HPC hardware. One way to think about Generic Retargetable vector-Level Dialect is that it operates on vector types that are multiples of a “good” vector size so the HW can efficiently implement a set of high-level primitives (e.g. vector<8x8x8x16xf32> when HW vector size is say vector<4x8xf32>).
Some notable vector sizes of interest include:
- CPU:
vector<HW_vector_size * k>,vector<core_count * k’ x HW_vector_size * k>andvector<socket_count x core_count * k’ x HW_vector_size * k> - GPU:
vector<warp_size * k>,vector<warp_size * k x float4>andvector<warp_size * k x 4 x 4 x 4>for tensor_core sizes, - Other accelerators: n-D
vectoras first-class citizens in the HW.
Depending on the target, ops on sizes that are not multiples of the HW vector size may either produce slow code (e.g. by going through LLVM legalization) or may not legalize at all (e.g. some unsupported accelerator X combination of ops and types).
Transformations Problems Avoided
A vector<16x32x64xf32> virtual vector is a coarse-grained type that can be “unrolled” to HW-specific sizes. The multi-dimensional unrolling factors are carried in the IR by the vector type. After unrolling, traditional instruction-level scheduling can be run.
The following key transformations (along with the supporting analyses and structural constraints) are completely avoided by operating on a vector ssa-value abstraction:
- Loop unroll and unroll-and-jam.
- Loop and load-store restructuring for register reuse.
- Load to store forwarding and Mem2reg.
- Coarsening (raising) from finer-grained
vectorform.
Note that “unrolling” in the context of vectors corresponds to partial loop unroll-and-jam and not full unrolling. As a consequence this is expected to compose with SW pipelining where applicable and does not result in ICache blow up.
The Big Out-Of-Scope Piece: Automatic Vectorization
One important piece not discussed here is automatic vectorization (automatically raising from scalar to n-D vector ops and types). The TL;DR is that when the first “super-vectorization” prototype was implemented, MLIR was nowhere near as mature as it is today. As we continue building more abstractions in VV -> HWV, there is an opportunity to revisit vectorization in MLIR.
Since this topic touches on codegen abstractions, it is technically out of the scope of this survey document but there is a lot to discuss in light of structured op type representations and how a vectorization transformation can be reused across dialects. In particular, MLIR allows the definition of dialects at arbitrary levels of granularity and lends itself favorably to progressive lowering. The argument can be made that automatic vectorization on a loops + ops abstraction is akin to raising structural information that has been lost. Instead, it is possible to revisit vectorization as simple pattern rewrites, provided the IR is in a suitable form. For instance, vectorizing a linalg.generic op whose semantics match a matmul can be done quite easily with a pattern. In fact this pattern is trivial to generalize to any type of contraction when targeting the vector.contract op, as well as to any field (+/*, min/+, max/+, or/and, logsumexp/+ ...) . In other words, by operating on a higher level of generic abstractions than affine loops, non-trivial transformations become significantly simpler and composable at a finer granularity.
Irrespective of the existence of an auto-vectorizer, one can build a notional vector language based on the VectorOps dialect and build end-to-end models with expressing vectors in the IR directly and simple pattern-rewrites. EDSCs provide a simple way of driving such a notional language directly in C++.
Bikeshed Naming Discussion
There are arguments against naming an n-D level of abstraction vector because most people associate it with 1-D vectors. On the other hand, vectors are first-class n-D values in MLIR. The alternative name Tile has been proposed, which conveys higher-D meaning. But it also is one of the most overloaded terms in compilers and hardware. For now, we generally use the n-D vector name and are open to better suggestions.
DeeperDive
This section describes the tradeoffs involved in lowering the MLIR n-D vector type and operations on it to LLVM-IR. Putting aside the LLVM Matrix proposal for now, this assumes LLVM only has built-in support for 1-D vector. The relationship with the LLVM Matrix proposal is discussed at the end of this document.
MLIR does not currently support dynamic vector sizes (i.e. SVE style) so the discussion is limited to static rank and static vector sizes (e.g. vector<4x8x16x32xf32>). This section discusses operations on vectors in LLVM and MLIR.
LLVM instructions are prefixed by the llvm. dialect prefix (e.g. llvm.insertvalue). Such ops operate exclusively on 1-D vectors and aggregates following the LLVM LangRef. MLIR operations are prefixed by the vector. dialect prefix (e.g. vector.insertelement). Such ops operate exclusively on MLIR n-D vector types.
Alternatives For Lowering an n-D Vector Type to LLVM
Consider a vector of rank n with static sizes {s_0, ... s_{n-1}} (i.e. an MLIR vector<s_0x...s_{n-1}xf32>). Lowering such an n-D MLIR vector type to an LLVM descriptor can be done by either:
- Flattening to a
1-Dvector:!llvm<"(s_0*...*s_{n-1})xfloat">in the MLIR LLVM dialect. - Nested aggregate type of
1-Dvector:!llvm."[s_0x[s_1x[...<s_{n-1}xf32>]]]">in the MLIR LLVM dialect. - A mix of both.
There are multiple tradeoffs involved in choosing one or the other that we discuss. It is important to note that “a mix of both” immediately reduces to “nested aggregate type of 1-D vector” with a vector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32> operation, that flattens the most “k” minor dimensions.
Constraints Inherited from LLVM (see LangRef)
The first constraint was already mentioned: LLVM only supports 1-D vector types natively. Additional constraints are related to the difference in LLVM between vector and aggregate types: “Aggregate Types are a subset of derived types that can contain multiple member types. Arrays and structs are aggregate types. Vectors are not considered to be aggregate types.”.
This distinction is also reflected in some of the operations. For 1-D vectors, the operations llvm.extractelement, llvm.insertelement, and llvm.shufflevector apply, with direct support for dynamic indices. For n-D vectors with n>1, and thus aggregate types at LLVM level, the more restrictive operations llvm.extractvalue and llvm.insertvalue apply, which only accept static indices. There is no direct shuffling support for aggregate types.
The next sentence illustrates a recurrent tradeoff, also found in MLIR, between “value types” (subject to SSA use-def chains) and “memory types” (subject to aliasing and side-effects): “Structures in memory are accessed using ‘load’ and ‘store’ by getting a pointer to a field with the llvm.getelementptr instruction. Structures in registers are accessed using the llvm.extractvalue and llvm.insertvalue instructions.”
When transposing this to MLIR, llvm.getelementptr works on pointers to n-D vectors in memory. For n-D, vectors values that live in registers we can use vector.extract and vector.insert which do not accept dynamic indices. Note that this is consistent with hardware considerations as discussed below.
An alternative is to use an LLVM 1-D vector type for which one can use llvm.extractelement, llvm.insertelement and llvm.shufflevector. These operations accept dynamic indices. The implication is that one has to use a flattened lowering of an MLIR n-D vector to an LLVM 1-D vector.
There are multiple tradeoffs involved that mix implications on the programming model, execution on actual HW and what is visible or hidden from codegen. They are discussed in the following sections.
Nested Aggregate
Pros:
- Natural encoding n-D vector -> (n-1)-D aggregate over 1-D vector.
- No need for linearization / delinearization logic inserted everywhere.
llvm.insertvalue,llvm.extractvalueof(n-k)-Daggregate is natural.llvm.insertelement,llvm.extractelement,llvm.shufflevectorover1-Dvector type is natural.
Cons:
llvm.insertvalue/llvm.extractvaluedoes not accept dynamic indices but only static ones.- Dynamic indexing on the non-most-minor dimension requires roundtrips to memory.
- Special intrinsics and native instructions in LLVM operate on
1-Dvectors. This is not expected to be a practical limitation thanks to avector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32>operation, that flattens the most minor dimensions (see the bigger picture in implications on codegen).
Flattened 1-D Vector Type
Pros:
insertelement/extractelement/shufflevectorwith dynamic indexing is possible over the whole loweredn-Dvector type.- Supports special intrinsics and native operations.
Cons:
- Requires linearization/delinearization logic everywhere, translations are complex.
- Hides away the real HW structure behind dynamic indexing: at the end of the day, HW vector sizes are generally fixed and multiple vectors will be needed to hold a vector that is larger than the HW.
- Unlikely peephole optimizations will result in good code: arbitrary dynamic accesses, especially at HW vector boundaries unlikely to result in regular patterns.
Discussion
HW Vectors and Implications on the SW and the Programming Model
As of today, the LLVM model only support 1-D vector types. This is unsurprising because historically, the vast majority of HW only supports 1-D vector registers. We note that multiple HW vendors are in the process of evolving to higher-dimensional physical vectors.
In the following discussion, let's assume the HW vector size is 1-D and the SW vector size is n-D, with n >= 1. The same discussion would apply with 2-D HW vector size and n >= 2. In this context, most HW exhibit a vector register file. The number of such vectors is fixed. Depending on the rank and sizes of the SW vector abstraction and the HW vector sizes and number of registers, an n-D SW vector type may be materialized by a mix of multiple 1-D HW vector registers + memory locations at a given point in time.
The implication of the physical HW constraints on the programming model are that one cannot index dynamically across hardware registers: a register file can generally not be indexed dynamically. This is because the register number is fixed and one either needs to unroll explicitly to obtain fixed register numbers or go through memory. This is a constraint familiar to CUDA programmers: when declaring a private float a[4]; and subsequently indexing with a dynamic value results in so-called local memory usage (i.e. roundtripping to memory).
Implication on codegen
MLIR n-D vector types are currently represented as (n-1)-D arrays of 1-D vectors when lowered to LLVM. This introduces the consequences on static vs dynamic indexing discussed previously: extractelement, insertelement and shufflevector on n-D vectors in MLIR only support static indices. Dynamic indices are only supported on the most minor 1-D vector but not the outer (n-1)-D. For other cases, explicit load / stores are required.
The implications on codegen are as follows:
- Loops around
vectorvalues are indirect addressing of vector values, they must operate on explicit load / store operations overn-Dvector types. - Once an
n-Dvectortype is loaded into an SSA value (that may or may not live innregisters, with or without spilling, when eventually lowered), it may be unrolled to smallerk-Dvectortypes and operations that correspond to the HW. This level of MLIR codegen is related to register allocation and spilling that occur much later in the LLVM pipeline. - HW may support >1-D vectors with intrinsics for indirect addressing within these vectors. These can be targeted thanks to explicit
vector_castoperations from MLIRk-Dvector types and operations to LLVM1-Dvectors + intrinsics.
Alternatively, we argue that directly lowering to a linearized abstraction hides away the codegen complexities related to memory accesses by giving a false impression of magical dynamic indexing across registers. Instead we prefer to make those very explicit in MLIR and allow codegen to explore tradeoffs. Different HW will require different tradeoffs in the sizes involved in steps 1., 2. and 3.
Decisions made at the MLIR level will have implications at a much later stage in LLVM (after register allocation). We do not envision to expose concerns related to modeling of register allocation and spilling to MLIR explicitly. Instead, each target will expose a set of “good” target operations and n-D vector types, associated with costs that PatterRewriters at the MLIR level will be able to target. Such costs at the MLIR level will be abstract and used for ranking, not for accurate performance modeling. In the future such costs will be learned.
Implication on Lowering to Accelerators
To target accelerators that support higher dimensional vectors natively, we can start from either 1-D or n-D vectors in MLIR and use vector.cast to flatten the most minor dimensions to 1-D vector<Kxf32> where K is an appropriate constant. Then, the existing lowering to LLVM-IR immediately applies, with extensions for accelerator-specific intrinsics.
It is the role of an Accelerator-specific vector dialect (see codegen flow in the figure above) to lower the vector.cast. Accelerator -> LLVM lowering would then consist of a bunch of Accelerator -> Accelerator rewrites to perform the casts composed with Accelerator -> LLVM conversions + intrinsics that operate on 1-D vector<Kxf32>.
Some of those rewrites may need extra handling, especially if a reduction is involved. For example, vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32> when K != K1 * … * Kn and some arbitrary irregular vector.cast %0: vector<4x4x17xf32> to vector<Kxf32> may introduce masking and intra-vector shuffling that may not be worthwhile or even feasible, i.e. infinite cost.
However vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32> when K = K1 * … * Kn should be close to a noop.
As we start building accelerator-specific abstractions, we hope to achieve retargetable codegen: the same infra is used for CPU, GPU and accelerators with extra MLIR patterns and costs.
Implication on calling external functions that operate on vectors
It is possible (likely) that we additionally need to linearize when calling an external function.
Relationship to LLVM matrix type proposal.
The LLVM matrix proposal was formulated 1 year ago but seemed to be somewhat stalled until recently. In its current form, it is limited to 2-D matrix types and operations are implemented with LLVM intrinsics. In contrast, MLIR sits at a higher level of abstraction and allows the lowering of generic operations on generic n-D vector types from MLIR to aggregates of 1-D LLVM vectors. In the future, it could make sense to lower to the LLVM matrix abstraction also for CPU even though MLIR will continue needing higher level abstractions.
On the other hand, one should note that as MLIR is moving to LLVM, this document could become the unifying abstraction that people should target for 1-D vectors and the LLVM matrix proposal can be viewed as a subset of this work.
Conclusion
The flattened 1-D vector design in the LLVM matrix proposal is good in a HW-specific world with special intrinsics. This is a good abstraction for register allocation, Instruction-Level-Parallelism and SoftWare-Pipelining/Modulo Scheduling optimizations at the register level. However MLIR codegen operates at a higher level of abstraction where we want to target operations on coarser-grained vectors than the HW size and on which unroll-and-jam is applied and patterns across multiple HW vectors can be matched.
This makes “nested aggregate type of 1-D vector” an appealing abstraction for lowering from MLIR because:
- it does not hide complexity related to the buffer vs value semantics and the memory subsystem and
- it does not rely on LLVM to magically make all the things work from a too low-level abstraction.
The use of special intrinsics in a 1-D LLVM world is still available thanks to an explicit vector.cast op.
Operations
[include “Dialects/VectorOps.md”]